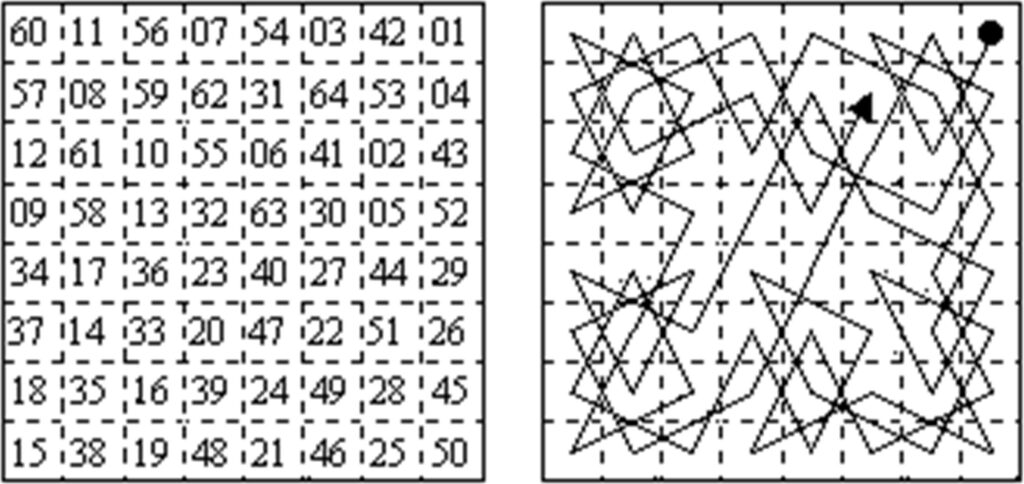
Historical Depth: The Knight’s Tour is a mathematical sequence in which a knight visits every single square on a chessboard exactly once. It is both a strategic challenge and a classic problem in recreational mathematics.
Origins:
This problem is far from a modern discovery. The earliest known solutions date back to the 9th century, provided by masters from Baghdad such as Al-Adli and As-Suli. Furthermore, in 9th-century Indian literature, the Kashmiri poet Rudrata demonstrated this mathematical aesthetic in his work Kavyalankara, where he composed a poem that followed the sequence of a knight’s tour.
Western Literature:
In the 13th century, King Alfonso X of Castile featured complex maneuvers based on the knight’s movement in his famous Libro de los Juegos (Book of Games). However, the modern mathematical foundation of the problem was laid in 1759 by Leonhard Euler, whose analysis is now recognized as one of the cornerstones of Graph Theory.
Characteristics:
* Closed (Re-entrant) Tour: If the knight finishes on a square that is exactly one knight’s move away from the starting square, allowing it to immediately begin the tour again.
Open Tour:
If the knight visits every square but ends on a square from which it cannot reach the starting point in a single move.

Posed by Max Bezzel in 1848 and drawing the attention of geniuses such as Carl Friedrich Gauss, this problem was transformed into a “programming manifesto” in the 1970s by one of the fathers of modern computer science, Edsger W. Dijkstra.
In his seminal work, Notes on Structured Programming (1972), Dijkstra utilized the 8 Queens Problem to demonstrate how an algorithm can be systematically constructed through a process he called “step-wise refinement.”
The Power of Backtracking:
According to Dijkstra, this approach represents the first major milestone in refining the “trial-and-error” process into a flawless logical sequence that a co

Legend and Origin:
According to the story, when the inventor of chess, Sissa bin Dahir, presented the game to the King of India, the King asked him what reward he would like. Sissa made a seemingly modest request: “I want one grain of wheat for the first square of the chessboard, two for the second, four for the third, and for each subsequent square, twice the amount of the previous one.” The King initially dismissed this request, thinking it was just “a handful of wheat”; however, when the calculation began, it became clear that neither the treasury nor the world’s entire wheat stocks would be sufficient to fulfill this demand.
Historical Record: Ibn Khallikan (1256)
The first known written record of this famous story was documented in 1256 by the renowned biographer and historian Ibn Khallikan. Ibn Khallikan incorporated this event into his work not merely as a tale, but as evidence of how mathematics pushes the boundaries of the imagination.
Mathematical Reality:
This request made for the 64 squares on the chessboard is the purest example of geometric progression (exponential growth). The amount on each square is calculated using the formula $2^{n-1}$. The equation providing the total amount of wheat is as follows:
$$S = \sum_{i=0}^{63} 2^i = 2^{64} – 1$$
The massive figure resulting from this calculation is:
18,446,744,073,709,551,615
Why Is It So Important?
Strategic Lesson: This problem is an ancient lesson of wisdom that teaches leaders and strategists how small changes (“doubling”) can transform into uncontrollable forces over time.